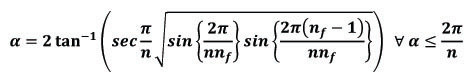Mathematical Legacy of Harish Chandra Rajpoot

Harish Chandra Rajpoot (Mumbai, India)
Harish Chandra Rajpoot (Mumbai, India)

Education

Doctor of Philosophy (Mechanical Engineering)

Indian Institute of Technology Bombay

 

M. Tech. (Production Engineering) ||9.12/10||

Indian Institute of Technology Delhi

 

B.Tech (Mechanical Engineering) ||78.6/100||

M.M.M. University of Technology

Gorakhpur (UP) India

  

Contributions

          Mathematical Achievements
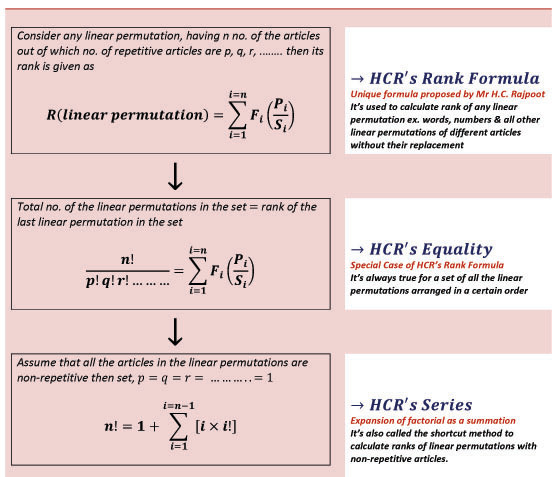
  • HCR's Rank Formula (Algebra)
  • Linear Permutations (Hierarchical Order)
  • Circular Permutations (Hierarchical Order)
  • Factorial as a summation (Number Theory)
  • HCR's Corollary of Solid Angle (3-D Geometry)
  • Analysis of 2-D figures
  • Analysis of 3-D figures
  • Graphics Theory of Solid Angle (Geometry & Radiometry)
  • HCR's Approximation Theorem (Geometry & Radiometry)
  • HCR's Axioms of Trigonometry & Geometry.
  • Analysis of Voids in Crystalline Unit Cells 
  • Modification of Lambert's Cosine Law (Photometry)
  • Analysis of Elliptical section of Right Cone (2-D Geometry)
  • HCR's Theory of Polygon (solid angle subtended by any polygonal plane at any point in the space)
  • HCR's Infinite series (volume & surface area of oblique frustum of right circular cone)
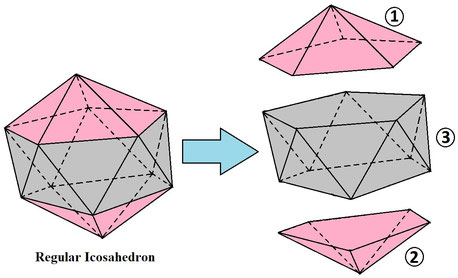
  • HCR's Formula for platonic solids or regular polyhedrons
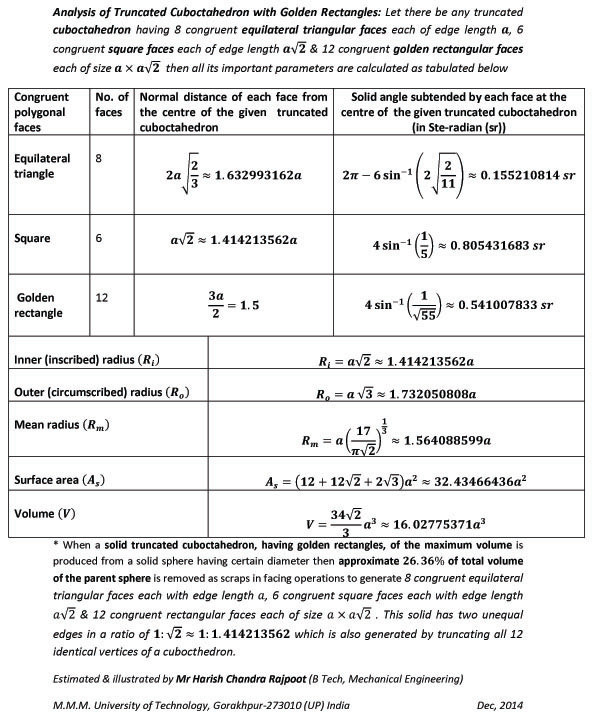
  • Mathematical analysis of all 13 Archimedean solids 
  • Analysis of non-uniform polyhedrons with right kite-faces
  • HCR's formula for regular spherical polygons
  • HCR's cosine formula to compute angle between the chords of two concurrent great circle arcs on a sphere
  • HCR's inverse cosine formula for computing geographical distance between any two points on the globe
  • Analysis of elliptical & hyperbolic sections of a right circular cone
  • derived formula to analytically compute the solid angle subtended by a tetrahedron at its vertex & solid angle subtended at the origin by any triangle given position vectors of vertices
  • derived formula to analytically compute volume, in-radius & circum-radius of a disphenoid.
  • derived governing equation/relation of a disphenoid
  • mathematically proved that in-center, circum-center & centroid of a disphenoid are always coincident
  • derived formula to compute area of spherical triangle for given aperture angles subtended by the sides
  • gave three proofs of Apollonius theorem
  • derived HCR's Theorem & Corollary, and applied for designing pyramidal flat containers with n-gonal bases, right pyramids and polyhedrons
  • derived analytic formula for a rhombic dodecahedron.
  • discovered a new polyhedron by truncating a rhombic dodecahedron
  • proposed mathematical formula in differential form to analytically compute the strength of magnetic field generated by rotating electric charge. 
  • derived recurrence relations and generalized formula for circle packing in the square, sector, hexagon, and circle
  • mathematically proved that the maximum possible packing fraction of identical circles of a finite radius on an infinite plane is 90.69%.
  • proposed a new term 'Circum-inscribed Polygon' and derived AM-GM formula for circum-inscribed (C-I) trapezium. 
  • derived generalized formula for regular n-gonal right antiprism using HCR's Theory of Polygon

Philosophy

 

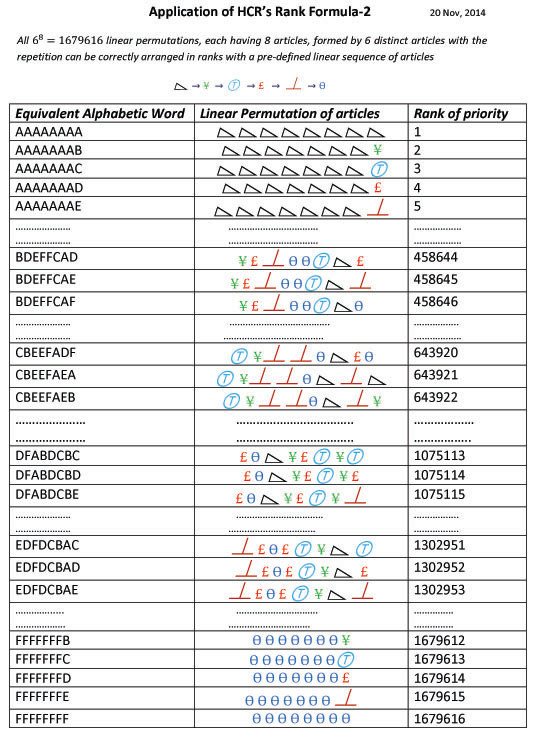
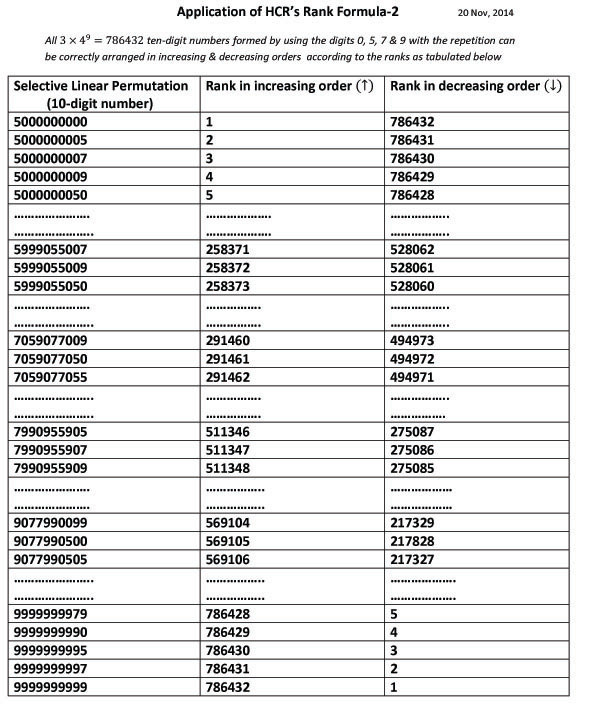
It's been seen till 20th century in the field of Algebra, there had not been derived such simplest & the most versatile formula which can mathematically calculate the order of priority (hierarchical rank)  of any linear permutation (as well as circular permutation under certain conditions) randomly selected from a set of all the linear permutations consisting of identical, non-identical, mixture of algebraic & non-algebraic and all other real and imaginary objects in the world. The well known examples of linear permutations are alphabetic words & numbers which have pre-defined linear sequence i.e. alphabetic order & numeric order respectively. But there are certain other objects of various kinds which do not have any pre-defined sequence for their arrangements. This means that one can arrangement the non-algebraic elements/things in any sequence or order as per one's desire. Once the sequence of non-algebraic objects is defined, it  becomes quite simple to arrange their all possible linear or circular permutations in the correct hierarchical order or rank based on the pre-defined sequence of selected algebraic or non algebraic objects or elements. He carried out an extensive study on the linear permutations of certain articles especially alphabetic words & numbers. As a result of his in-depth studies, he set forth a universal formula entitled 'HCR's Rank or Series Formula' merely by logic and without using any previously established mathematical formula.  Rank formula is a logic which holds true for all the linear permutations as well as the circular permutations under certain conditions. This universal formula equally holds true for the linear permutations of all kinds of objects i.e. letters, numbers and all other objects/things (living or non-living). 

 

Publication: www.researchpublish.com

 

Title: HCR's Rank or Series Formula

 

Author: Harish Chandra Rajpoot

 

Manuscript ID: 004022014A

 

Date of Certification: 9 Feb, 2014

 

Download
HCR's Hand Book (Formula of Advanced Geometry by H.C. Rajpoot)
All the standard formula from 'Advanced Geometry' by the author Mr H.C. Rajpoot have been included in this book. These formula are related to the solid geometry dealing with the 2-D & 3-D figures in the space & miscellaneous articles in Trigonometry & Geometry. These are useful the standard formula to be remembered for case studies & practical applications. Although, all the formula for the plane figures (i.e. planes bounded by the straight lines only) can be derived by using standard formula of right triangle that has been explained in details in "HCR's Theory of Polygon" published with International Journal of Mathematics & Physical Sciences Research in Oct, 2014.
And the analysis of oblique frustum of right circular cone has been explained in his research paper 'HCR's Infinite-series' published with IJMPSR
HCR's Hand Book.pdf
Adobe Acrobat Document 3.4 MB
Download
Download
Competitive questions from Book 'Electro-Magnetism' (Magnetic Field Generated by Rotating Electric Charge)
This is a small part of full text book 'Electro-Magnetism' which involves the solved examples and the competitive questions based on the concepts and mathematical formula in Physics derived in the original book written by H C Rajpoot published with Notion Press in Feb, 2020.
E-Book_ElectroMagnetism by HCRajpoot-202
Adobe Acrobat Document 917.1 KB
Download
The things which are absolutely negligible either do not exist or are nothing like zero in the context of mathematics. (26/01/2023)
The things which are absolutely negligible either do not exist or are nothing like zero in the context of mathematics. (26/01/2023)
Conclusive Statement (15/01/2023)
Conclusive Statement (15/01/2023)
Mr H.C. Rajpoot (B Tech, ME) M.M.M. University of Technology, Gorakhpur-273010 (UP) India. Date: 10 Jan, 2014
Mr H.C. Rajpoot (B Tech, ME) M.M.M. University of Technology, Gorakhpur-273010 (UP) India. Date: 10 Jan, 2014
Mr H. C. Rajpoot authored his first book 'Advanced Geometry' in Mathematics in April, 2013 published with Notion Press, Chennai, India
Mr H. C. Rajpoot authored his first book 'Advanced Geometry' in Mathematics in April, 2013 published with Notion Press, Chennai, India
Mr H. C. Rajpoot authored a new book 'Electro-Magnetism' in Theoretical Physics in Feb, 2020 published with Notion Press, Chennai, India
Mr H. C. Rajpoot authored a new book 'Electro-Magnetism' in Theoretical Physics in Feb, 2020 published with Notion Press, Chennai, India
Mr H. C. Rajpoot authored a new book 'Electro-Magnetism' in Theoretical Physics in Feb, 2020 published with Amazon
Mr H. C. Rajpoot authored a new book 'Electro-Magnetism' in Theoretical Physics in Feb, 2020 published with Amazon
HCR's Infinite or Convergence series
HCR's Infinite or Convergence series
Application of HCR's Rank Formula-2 on linear permutations with repetition of articles
Application of HCR's Rank Formula-2 on linear permutations with repetition of articles

HCR's Mathematical legacy ©Harish Chandra Rajpoot

Advanced Geometry by Harish Chandra Rajpoot (HCR's research book published by Notion Press in March, 2014)
www.notionpress.com
Mr H. C. Rajpoot, Master of Technology in Production Engineering at Indian Institute of Technology Delhi. 16 Aug, 2019
Mr H. C. Rajpoot, Master of Technology in Production Engineering at Indian Institute of Technology Delhi. 16 Aug, 2019
He handled the complete transmission system of all terrain vehicle like mechanism of gear change, location of gear lever, accelerator, break, clutch. He also collaborated in suspension system, drilling, grinding, cutting. welding, finishing etc.
Mr H.C. Rajpoot with ATV (manufactured by him along with his 19 team members @ his college MMMEC) in a Science Congress ever first in U.P. state held at D.D.U. Gorakhpur (UP), 2 March, 2013

HCR's Rank or Series Formula (Certified by International Journal of Mathematics & Physical Sciences Research in Feb, 2014)
www.researchpublish.com
HCR's Series (Expansion of Factorial of any Natural Number as Summation) Certified by International Organization of Scientific Research in March, 2014
www.iosrjournals.org
Certificate of Publication of Paper entitled 'HCR's THEORY OF POLYGON' published by International Journal of Mathematics & Physical Sciences Research, 12 Oct, 2014 (website: www.researchpublish.com)
Certificate of Publication of Paper entitled 'HCR's THEORY OF POLYGON' published by International Journal of Mathematics & Physical Sciences Research, 12 Oct, 2014 (website: www.researchpublish.com)
Certificate of Publication of Paper entitled 'HCR's Infinite-series' published by International Journal of Mathematics & Physical Sciences Research, 2 Oct, 2014 (website: www.researchpublish.com)
Certificate of Publication of Paper entitled 'HCR's Infinite-series' published by International Journal of Mathematics & Physical Sciences Research, 2 Oct, 2014 (website: www.researchpublish.com)
HCR's Rank Formula-2 used to calculate rank of any linear permutation for repetition of articles
HCR's Rank Formula-2 used to calculate rank of any linear permutation for repetition of articles
HCR's Rank Formula applied on the color property of articles to calculate ranks & arrange them in correct order
HCR's Rank Formula applied on the color property of articles to calculate ranks & arrange them in correct order
HCR's Rank Formula-2 applied on the linear permutations of non-algebraic articles to calculate the ranks & arrange all those in mathematical correct order
HCR's Rank Formula-2 applied on the linear permutations of non-algebraic articles to calculate the ranks & arrange all those in mathematical correct order
Application of HCR's Rank Formula-2 on the numbers with zero & non-zero digits
Application of HCR's Rank Formula-2 on the numbers with zero & non-zero digits
Solid angle covered by a regular pentagonal plane derived by using HCR's Theory of Polygon-2014
Solid angle covered by a regular pentagonal plane derived by using HCR's Theory of Polygon-2014
Solid angle covered by a regular hexagonal plane derived by using HCR's Theory of Polygon-2014
Solid angle covered by a regular hexagonal plane derived by using HCR's Theory of Polygon-2014
Derivation by Mr H. C. Rajpoot for the solid angle subtended by a regular heptagon using HCR's Theory of Polygon
Derivation by Mr H. C. Rajpoot for the solid angle subtended by a regular heptagon using HCR's Theory of Polygon
Derivation by H. C. Rajpoot for solid angle covered by a regular octagonal plane
Derivation by H. C. Rajpoot for solid angle covered by a regular octagonal plane
Verification of HCR's Rank Formula derived by Mr H. C. Rajpoot in Feb, 2010
Verification of HCR's Rank Formula derived by Mr H. C. Rajpoot in Feb, 2010
These are some important estimations made by Mr H. C. Rajpoot
These are some important estimations made by Mr H. C. Rajpoot
HCR's Series (expansion of factorial of any number as a summation ) is derived from HCR's Rank Formula (used to calculate rank of any linear permutation when the replacement of articles is not there in the linear permutations of a set) applying certain co
HCR's Series (expansion of factorial of any number as a summation ) is derived from HCR's Rank Formula (used to calculate rank of any linear permutation when the replacement of articles is not there in the linear permutations of a set) applying certain co
HCR’s Inverse Cosine Formula derived by Mr H.C. Rajpoot is a trigonometric relation of four variables/angles. It is applicable for any three straight lines or planes, either co-planar or non-coplanar, intersecting each other at a single point in the space
HCR’s Inverse Cosine Formula derived by Mr H.C. Rajpoot is a trigonometric relation of four variables/angles. It is applicable for any three straight lines or planes, either co-planar or non-coplanar, intersecting each other at a single point in the space
This formula was derived by Mr H.C. Rajpoot by applying his "Theory of Polygon" to calculate all the important parameters of any regular n-polyhedron such as inner radius, outer radius, mean radius, surface area & volume. This formula is general in form.
This formula was derived by Mr H.C. Rajpoot by applying his "Theory of Polygon" to calculate all the important parameters of any regular n-polyhedron such as inner radius, outer radius, mean radius, surface area & volume. This formula is general in form.
Application of H. Rajpoot's Formula on a regular tetrahedron to calculate all the important parameters i.e. inner radius, outer radius, mean radius, surface area & volume only by measuring its edge length.
Application of H. Rajpoot's Formula on a regular tetrahedron to calculate all the important parameters i.e. inner radius, outer radius, mean radius, surface area & volume only by measuring its edge length.
All the important parameters of a truncated icosahedron such as normal distances & solid angles of the faces, inner radius, outer radius, mean radius, surface area & volume have been calculated by using HCR's formula for regular polyhedrons (all five plat
All the important parameters of a truncated icosahedron such as normal distances & solid angles of the faces, inner radius, outer radius, mean radius, surface area & volume have been calculated by using HCR's formula for regular polyhedrons (all five plat
Table of all the important parameters of a truncated tetrahedron (having 4 congruent equilateral triangular & 4 congruent regular hexagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner radius, o
Table of all the important parameters of a truncated tetrahedron (having 4 congruent equilateral triangular & 4 congruent regular hexagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner radius, o
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
HCR's formula for all five platonic solids
HCR's formula for all five platonic solids
Table of all the important parameters of a truncated hexahedron (having 8 congruent equilateral triangular & 6 congruent regular octagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
Table of all the important parameters of a truncated hexahedron (having 8 congruent equilateral triangular & 6 congruent regular octagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
Table of all the important parameters of a cuboctahedron (Archimedean solid having 8 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
Table of all the important parameters of a cuboctahedron (Archimedean solid having 8 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
All the important parameters of an icosidodecahedron (having 20 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
All the important parameters of an icosidodecahedron (having 20 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
such as normal distances & solid angles subtended by the faces, inner radius, outer radius, mean radius, surface area & volume calculated by using HCR's formula for regular polyhedrons. It can be used in analysis, designing & modelling of polyhedrons.
Table of all the important parameters of the rhombicosidodecahedron (an Archimedean solid having 20 congruent equilateral triangular, 30 congruent square & 12 congruent regular pentagonal faces each of equal edge length)
Table of all the important parameters of a truncated icosidodecahedron (having 20 congruent equilateral triangular faces, 30 congruent golden rectangular faces & 12 congruent regular pentagonal faces) such as normal distances & solid angles by the faces
Table of all the important parameters of a truncated icosidodecahedron (having 20 congruent equilateral triangular faces, 30 congruent golden rectangular faces & 12 congruent regular pentagonal faces) such as normal distances & solid angles by the faces
Table of all the important parameters of the great rhombicosidodecahedron (the largest Archimedean solid having 30 congruent square, 20 congruent regular hexagonal & 12 congruent regular decagonal faces each of equal edge length)
Table of all the important parameters of the great rhombicosidodecahedron (the largest Archimedean solid having 30 congruent square, 20 congruent regular hexagonal & 12 congruent regular decagonal faces each of equal edge length)
Table of all the important parameters of a small rhombicuboctahedron (an Archimedean solid having 8 congruent equilateral triangular & 18 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces,
Table of all the important parameters of a small rhombicuboctahedron (an Archimedean solid having 8 congruent equilateral triangular & 18 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces,
Table of the important parameters of Great Rhombicuboctahedron (an Archimedean solid having 12 congruent square, 8 congruent regular hexagonal & 6 regular octagonal faces each of equal edge length) such as normal distances & solid angles by the faces.
Table of the important parameters of Great Rhombicuboctahedron (an Archimedean solid having 12 congruent square, 8 congruent regular hexagonal & 6 regular octagonal faces each of equal edge length) such as normal distances & solid angles by the faces.
Table of the important parameters of a truncated cuboctahedron (having 8 congruent equilateral triangular, 6 congruent square & 12 congruent golden rectangular faces) such as normal distances & solid angles subtended by the faces.
Table of the important parameters of a truncated cuboctahedron (having 8 congruent equilateral triangular, 6 congruent square & 12 congruent golden rectangular faces) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub cube (an Archimedean solid having 32 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub cube (an Archimedean solid having 32 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub dodecahedron (an Archimedean solid having 80 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub dodecahedron (an Archimedean solid having 80 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
Table of all the important parameters of any regular spherical polygon such as solid angle subtended at the center, area, length of side, interior angle etc. derived by Mr H.C. Rajpoot by using simple geometry & trigonometry.
Table of all the important parameters of any regular spherical polygon such as solid angle subtended at the center, area, length of side, interior angle etc. derived by Mr H.C. Rajpoot by using simple geometry & trigonometry.
Table of all the important parameters of a decahedron having 10 congruent faces each as a right kite to calculate normal distance of each face from the center, inscribed radius, circumscribed radius, mean radius, surface area & volume.
Table of all the important parameters of a decahedron having 10 congruent faces each as a right kite to calculate normal distance of each face from the center, inscribed radius, circumscribed radius, mean radius, surface area & volume.
Table of the important parameters of a uniform tetradecahedron, having 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface with certain radius, derived by the author by applying "HCR's Theory.
Table of the important parameters of a uniform tetradecahedron, having 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface with certain radius, derived by the author by applying "HCR's Theory.
Table of the formula generalized by the author which are applicable to calculate the important parameters, of any uniform polyhedron having 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces, 5n edges & 3n vertices lying on a sphere
Table of the formula generalized by the author which are applicable to calculate the important parameters, of any uniform polyhedron having 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces, 5n edges & 3n vertices lying on a sphere
Generalized formula to calculate area covered by any spherical rectangle having length l & width b each as a great circle arc on a sphere with a radius R" derived by Mr H.C. Rajpoot applying his "Theory of Polygon" for solid angle.
Generalized formula to calculate area covered by any spherical rectangle having length l & width b each as a great circle arc on a sphere with a radius R" derived by Mr H.C. Rajpoot applying his "Theory of Polygon" for solid angle.
The solid angles subtended at the vertices by all five platonic solids (regular polyhedrons) have been calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle. These are the standard values of solid angles for all platonic solids
The solid angles subtended at the vertices by all five platonic solids (regular polyhedrons) have been calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle. These are the standard values of solid angles for all platonic solids
Table of the generalized formula applicable on any uniform polyhedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface with a certain radius. These formula have been derived by the author Mr H.C. Rajpoot.
Table of the generalized formula applicable on any uniform polyhedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface with a certain radius. These formula have been derived by the author Mr H.C. Rajpoot.
Table for the important parameters for the identical circles touching one another on a whole (entire) spherical surface having certain radius such as flat radius & arc radius of each circle, total surface area & its percentage covered by all the circles.
Table for the important parameters for the identical circles touching one another on a whole (entire) spherical surface having certain radius such as flat radius & arc radius of each circle, total surface area & its percentage covered by all the circles.
Table of the generalized formula derived here by the author are applicable to locate any sphere, with a certain radius, resting in a vertex (corner) at which n no. of edges meet together at angle α between any two consecutive of them.
Table of the generalized formula derived here by the author are applicable to locate any sphere, with a certain radius, resting in a vertex (corner) at which n no. of edges meet together at angle α between any two consecutive of them.
Table for the formula generalized by the author to determine the important parameters for snugly packing the spheres in the vertices of all five platonic solids such as the radius of Nth sphere, total volume packed by all the spheres, packing ratio etc.
Table for the formula generalized by the author to determine the important parameters for snugly packing the spheres in the vertices of all five platonic solids such as the radius of Nth sphere, total volume packed by all the spheres, packing ratio etc.
Spherical Geometry by H.C. Rajpoot
HCR's Formula for Regular Spherical Polygon
This inequality had been derived from a general formula which always holds true for any three real positive numbers.
HCR's Inequality for three positive real numbers
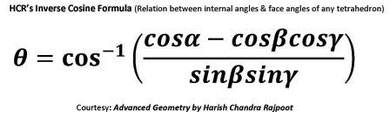
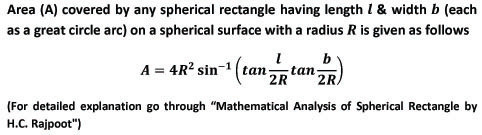
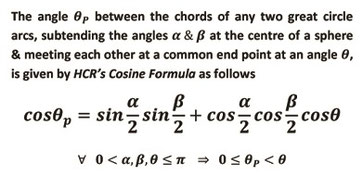
This formula is used to mathematically derive the analytic formula to compute distance between any two points on the sphere or globe given latitudes & longitudes. It is an important formula in Global Positioning System (GPS) to precisely compute distances
HCR's cosine formula to calculate the angle between the chords of any two great circle arcs meeting each other at a common end point at some angle
These are the most generalized formula to compute the volume & surface area of a right circular cone cut by a plane parallel to its symmetrical axis at a certain distance
Volume & surface area of a right circular cone cut by a plane parallel to its symmetrical axis (A cut cone with hyperbolic section)
General formula to compute the correct value of the solid angle subtended by any tetrahedron at its vertex when the angles between consecutive lateral edges meeting at that vertex are known
Solid angle subtended by any tetrahedron at its vertex given the angles between consecutive lateral edges meeting at that vertex
A general (analytic & precision) formula to compute the correct value of solid angle subtended by any triangle at the origin which is equally applicable in all the cases given the position vectors of all three vertices in 3D coordinate system.
Solid angle subtended at the origin by any triangle given the position vectors of its vertices
Formula of Disphenoid derived by H C Rajpoot
Formula/Governing Equation of Disphenoid (Isosceles Tetrahderom) derived by HCR
HCR's Theorem derived by H C Rajpoot
HCR's Theorem (Rotation of two co-planar planes, meeting at angle bisector, about their intersecting straight edges )
HCR's Corollary derived by H C Rajpoot
HCR's Corollary (Dihedral angle between two co-planar planes rotated about their intersecting straight edges )
Application of HCR's Theory of Polygon proposed by H C Rajpoot (year-2014)
Derivations of analytic formula for rhombicuboctahedron by applying HCR's Theory of Polygon proposed by H C Rajpoot
Mathematical discovery in 2D Geometry by H C Rajpoot -2021
Mathematically proved that the maximum possible packing fraction of identical circles of a finite radius over an infinite plane is 90.69%. 01 August, 2021.
Derivation of great circle distance formula in 3D Geometry by H C Rajpoot -Aug, 2016
Mathematical derivation of great-circle distance formula using HCR's inverse cosine formula and vectors
Mathematical discovery in 2D Geometry by H C Rajpoot -2021
Mathematical analysis of circum-inscribed (C-I) trapezium
Plane vs Solid Angle by H C Rajpoot -2022
Comparison between Plane Angle and Solid Angle
Polyhedron by H C Rajpoot -2023
Regular pentagonal right antiprism obtained by truncating a regular icosahedron
Polygonal Antiprism by H C Rajpoot -2023
Generalized formula of regular n-gonal right antiprism derived using HCR's Theory of Polygon
Application of HCR's Theory of Polygon
A regular pentagonal right antiprism is generated by truncating a regular icosahedron
Application of HCR's Theory of Polygon
A net of 10 regular triangular and 2 regular pentagonal faces is folded to generate a regular pentagonal right antiprism
Application of HCR's Theorem
A paper model of a pyramidal flat container with regular heptagonal base of desired dimensions & angle, crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem
Application of HCR's Theorem
A paper model of a pyramidal flat container with regular pentagonal base of desired dimensions & angle, crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem
Application of HCR's Theorem
A paper model of Polyhedron with two regular pentagonal and ten trapezoidal faces crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem
Application of HCR's Theory of Polygon
A paper model of rhombic dodecahedron with 12 congruent rhombic faces crafted manually by Mr H.C. Rajpoot. He marked all 14 vertices to truncate a rhombic dodecahedron.
Application of HCR's Theory of Polygon
Mr H.C. Rajpoot discovered and developed a new polyhedron (right) called 'Truncated Rhombic Dodecahedron (HCR's Polyhedron)' by truncating a rhombic dodecahedron (left)
Application of HCR's Theory of Polygon
A model of Regular Penta-decahedral Solar Dome of 5mm thick acrylic sheet having 15 regular triangular faces each with side 15 cm crafted by H C Rajpoot, 26 Oct, 2021.
H C Rajpoot @ IIT Delhi
3-D Model on Creo 5.0
H C Rajpoot @ IIT Bombay
Laser engraving on sodalime glass
Mr H. C. Rajpoot (DOB: 20 Jan, 1991), 12th Standard (Intermediate) @ Oxford Model Inter College, Syam Nagar, Kanpur (UP), India (March, 2009)
Mr H. C. Rajpoot (DOB: 20 Jan, 1991), 12th Standard (Intermediate) @ Oxford Model Inter College, Syam Nagar, Kanpur (UP), India (March, 2009)
Mr H. C. Rajpoot (Doctor of Philosophy @ IIT Bombay)
Mr H. C. Rajpoot (Doctor of Philosophy @ IIT Bombay)
Certificate of Best paper Award in Young Scholars' National Research Writing Competition 2021.
Certificate of Best paper Award in Young Scholars' National Research Writing Competition 2021.
Certificate of Excellence in Peer-Reviewing for contributing to the book chapter 'Time in Mathematical Models'
Certificate of Excellence in Peer-Reviewing for contributing to the book chapter 'Time in Mathematical Models'
Certificate of Editorial Board Membership
Certificate of Editorial Board Membership
Certificate of Authorship for publishing Advanced Geometry in Mathematics.
Certificate of Authorship for publishing Advanced Geometry in Mathematics.
Certificate of Authorship for publishing Electro-Magnetism in Physics.
Certificate of Authorship for publishing Electro-Magnetism in Physics.

This site has been created, in good faith, merely for keeping the records of biography, mathematical formulae & outstanding achievements of H.C. Rajpoot in the field of Mathematics specifically Algebra, Geometry, Trigonometry & Radiometry in Mathematical Physics.  

 

                                                                                             Copyright ©2014 - 2024. All Rights Reserved        

 

About | Privacy Policy | Sitemap
Log in Log out | Edit
Jimdo

You can do it, too! Sign up for free now at https://www.jimdo.com