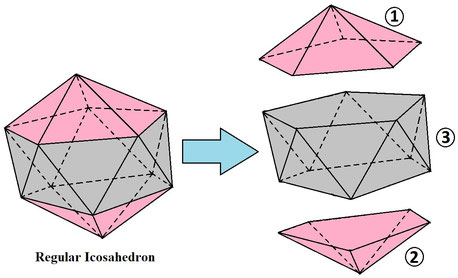
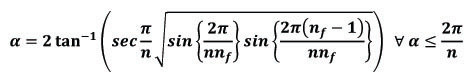HCR's Graphics Theory of Solid Angle - hcrajpoot

Solid Angle subtended by an octagonal plane

This theory is applied to find out the solid angle subtended by a polygonal plane at any point in the space under certain conditions.

This theory was published in International Journal of Mathematics & has been included in his book.

HCR's Mathematical legacy ©Harish Chandra Rajpoot

Advanced Geometry by Harish Chandra Rajpoot (HCR's research book published by Notion Press in March, 2014) — www.notionpress.com

Mr H. C. Rajpoot, Master of Technology in Production Engineering at Indian Institute of Technology Delhi. 16 Aug, 2019

He handled the complete transmission system of all terrain vehicle like mechanism of gear change, location of gear lever, accelerator, break, clutch. He also collaborated in suspension system, drilling, grinding, cutting. welding, finishing etc. — Mr H.C. Rajpoot with ATV (manufactured by him along with his 19 team members @ his college MMMEC) in a Science Congress ever first in U.P. state held at D.D.U. Gorakhpur (UP), 2 March, 2013

HCR's Rank or Series Formula (Certified by International Journal of Mathematics & Physical Sciences Research in Feb, 2014) — www.researchpublish.com

HCR's Series (Expansion of Factorial of any Natural Number as Summation) Certified by International Organization of Scientific Research in March, 2014 — www.iosrjournals.org

Certificate of Publication of Paper entitled 'HCR's THEORY OF POLYGON' published by International Journal of Mathematics & Physical Sciences Research, 12 Oct, 2014 (website: www.researchpublish.com)

Certificate of Publication of Paper entitled 'HCR's Infinite-series' published by International Journal of Mathematics & Physical Sciences Research, 2 Oct, 2014 (website: www.researchpublish.com)

HCR's Rank Formula-2 used to calculate rank of any linear permutation for repetition of articles

HCR's Rank Formula applied on the color property of articles to calculate ranks & arrange them in correct order

HCR's Rank Formula-2 applied on the linear permutations of non-algebraic articles to calculate the ranks & arrange all those in mathematical correct order

Application of HCR's Rank Formula-2 on the numbers with zero & non-zero digits

Solid angle covered by a regular pentagonal plane derived by using HCR's Theory of Polygon-2014

Solid angle covered by a regular hexagonal plane derived by using HCR's Theory of Polygon-2014

Derivation by Mr H. C. Rajpoot for the solid angle subtended by a regular heptagon using HCR's Theory of Polygon

Derivation by H. C. Rajpoot for solid angle covered by a regular octagonal plane

Verification of HCR's Rank Formula derived by Mr H. C. Rajpoot in Feb, 2010

These are some important estimations made by Mr H. C. Rajpoot

HCR's Series (expansion of factorial of any number as a summation ) is derived from HCR's Rank Formula (used to calculate rank of any linear permutation when the replacement of articles is not there in the linear permutations of a set) applying certain co

HCR’s Inverse Cosine Formula derived by Mr H.C. Rajpoot is a trigonometric relation of four variables/angles. It is applicable for any three straight lines or planes, either co-planar or non-coplanar, intersecting each other at a single point in the space

This formula was derived by Mr H.C. Rajpoot by applying his "Theory of Polygon" to calculate all the important parameters of any regular n-polyhedron such as inner radius, outer radius, mean radius, surface area & volume. This formula is general in form.

Application of H. Rajpoot's Formula on a regular tetrahedron to calculate all the important parameters i.e. inner radius, outer radius, mean radius, surface area & volume only by measuring its edge length.

All the important parameters of a truncated icosahedron such as normal distances & solid angles of the faces, inner radius, outer radius, mean radius, surface area & volume have been calculated by using HCR's formula for regular polyhedrons (all five plat

Table of all the important parameters of a truncated tetrahedron (having 4 congruent equilateral triangular & 4 congruent regular hexagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner radius, o

Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii

Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii

HCR's formula for all five platonic solids

Table of all the important parameters of a truncated hexahedron (having 8 congruent equilateral triangular & 6 congruent regular octagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii

Table of all the important parameters of a cuboctahedron (Archimedean solid having 8 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii

All the important parameters of an icosidodecahedron (having 20 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii

such as normal distances & solid angles subtended by the faces, inner radius, outer radius, mean radius, surface area & volume calculated by using HCR's formula for regular polyhedrons. It can be used in analysis, designing & modelling of polyhedrons. — Table of all the important parameters of the rhombicosidodecahedron (an Archimedean solid having 20 congruent equilateral triangular, 30 congruent square & 12 congruent regular pentagonal faces each of equal edge length)

Table of all the important parameters of a truncated icosidodecahedron (having 20 congruent equilateral triangular faces, 30 congruent golden rectangular faces & 12 congruent regular pentagonal faces) such as normal distances & solid angles by the faces

Table of all the important parameters of the great rhombicosidodecahedron (the largest Archimedean solid having 30 congruent square, 20 congruent regular hexagonal & 12 congruent regular decagonal faces each of equal edge length)

Table of all the important parameters of a small rhombicuboctahedron (an Archimedean solid having 8 congruent equilateral triangular & 18 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces,

Table of the important parameters of Great Rhombicuboctahedron (an Archimedean solid having 12 congruent square, 8 congruent regular hexagonal & 6 regular octagonal faces each of equal edge length) such as normal distances & solid angles by the faces.

Table of the important parameters of a truncated cuboctahedron (having 8 congruent equilateral triangular, 6 congruent square & 12 congruent golden rectangular faces) such as normal distances & solid angles subtended by the faces.

All the important parameters of a snub cube (an Archimedean solid having 32 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces.

All the important parameters of a snub dodecahedron (an Archimedean solid having 80 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces.

Table of all the important parameters of any regular spherical polygon such as solid angle subtended at the center, area, length of side, interior angle etc. derived by Mr H.C. Rajpoot by using simple geometry & trigonometry.

Table of all the important parameters of a decahedron having 10 congruent faces each as a right kite to calculate normal distance of each face from the center, inscribed radius, circumscribed radius, mean radius, surface area & volume.

Table of the important parameters of a uniform tetradecahedron, having 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface with certain radius, derived by the author by applying "HCR's Theory.

Table of the formula generalized by the author which are applicable to calculate the important parameters, of any uniform polyhedron having 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces, 5n edges & 3n vertices lying on a sphere

Generalized formula to calculate area covered by any spherical rectangle having length l & width b each as a great circle arc on a sphere with a radius R" derived by Mr H.C. Rajpoot applying his "Theory of Polygon" for solid angle.

The solid angles subtended at the vertices by all five platonic solids (regular polyhedrons) have been calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle. These are the standard values of solid angles for all platonic solids

Table of the generalized formula applicable on any uniform polyhedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface with a certain radius. These formula have been derived by the author Mr H.C. Rajpoot.

Table for the important parameters for the identical circles touching one another on a whole (entire) spherical surface having certain radius such as flat radius & arc radius of each circle, total surface area & its percentage covered by all the circles.

Table of the generalized formula derived here by the author are applicable to locate any sphere, with a certain radius, resting in a vertex (corner) at which n no. of edges meet together at angle α between any two consecutive of them.

Table for the formula generalized by the author to determine the important parameters for snugly packing the spheres in the vertices of all five platonic solids such as the radius of Nth sphere, total volume packed by all the spheres, packing ratio etc.

Spherical Geometry by H.C. Rajpoot — HCR's Formula for Regular Spherical Polygon

This inequality had been derived from a general formula which always holds true for any three real positive numbers. — HCR's Inequality for three positive real numbers

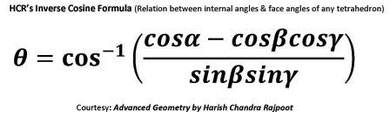
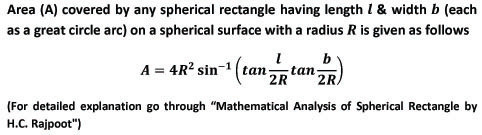
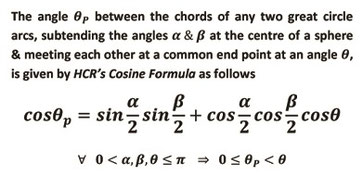
This formula is used to mathematically derive the analytic formula to compute distance between any two points on the sphere or globe given latitudes & longitudes. It is an important formula in Global Positioning System (GPS) to precisely compute distances — HCR's cosine formula to calculate the angle between the chords of any two great circle arcs meeting each other at a common end point at some angle

These are the most generalized formula to compute the volume & surface area of a right circular cone cut by a plane parallel to its symmetrical axis at a certain distance — Volume & surface area of a right circular cone cut by a plane parallel to its symmetrical axis (A cut cone with hyperbolic section)

General formula to compute the correct value of the solid angle subtended by any tetrahedron at its vertex when the angles between consecutive lateral edges meeting at that vertex are known — Solid angle subtended by any tetrahedron at its vertex given the angles between consecutive lateral edges meeting at that vertex

A general (analytic & precision) formula to compute the correct value of solid angle subtended by any triangle at the origin which is equally applicable in all the cases given the position vectors of all three vertices in 3D coordinate system. — Solid angle subtended at the origin by any triangle given the position vectors of its vertices

Formula of Disphenoid derived by H C Rajpoot — Formula/Governing Equation of Disphenoid (Isosceles Tetrahderom) derived by HCR

HCR's Theorem derived by H C Rajpoot — HCR's Theorem (Rotation of two co-planar planes, meeting at angle bisector, about their intersecting straight edges )

HCR's Corollary derived by H C Rajpoot — HCR's Corollary (Dihedral angle between two co-planar planes rotated about their intersecting straight edges )

Application of HCR's Theory of Polygon proposed by H C Rajpoot (year-2014) — Derivations of analytic formula for rhombicuboctahedron by applying HCR's Theory of Polygon proposed by H C Rajpoot

Mathematical discovery in 2D Geometry by H C Rajpoot -2021 — Mathematically proved that the maximum possible packing fraction of identical circles of a finite radius over an infinite plane is 90.69%. 01 August, 2021.

Derivation of great circle distance formula in 3D Geometry by H C Rajpoot -Aug, 2016 — Mathematical derivation of great-circle distance formula using HCR's inverse cosine formula and vectors

Mathematical discovery in 2D Geometry by H C Rajpoot -2021 — Mathematical analysis of circum-inscribed (C-I) trapezium

Plane vs Solid Angle by H C Rajpoot -2022 — Comparison between Plane Angle and Solid Angle

Polyhedron by H C Rajpoot -2023 — Regular pentagonal right antiprism obtained by truncating a regular icosahedron

Polygonal Antiprism by H C Rajpoot -2023 — Generalized formula of regular n-gonal right antiprism derived using HCR's Theory of Polygon

Application of HCR's Theory of Polygon — A regular pentagonal right antiprism is generated by truncating a regular icosahedron

Application of HCR's Theory of Polygon — A net of 10 regular triangular and 2 regular pentagonal faces is folded to generate a regular pentagonal right antiprism

Application of HCR's Theorem — A paper model of a pyramidal flat container with regular heptagonal base of desired dimensions & angle, crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem

Application of HCR's Theorem — A paper model of a pyramidal flat container with regular pentagonal base of desired dimensions & angle, crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem

Application of HCR's Theorem — A paper model of Polyhedron with two regular pentagonal and ten trapezoidal faces crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem

Application of HCR's Theory of Polygon — A paper model of rhombic dodecahedron with 12 congruent rhombic faces crafted manually by Mr H.C. Rajpoot. He marked all 14 vertices to truncate a rhombic dodecahedron.

Application of HCR's Theory of Polygon — Mr H.C. Rajpoot discovered and developed a new polyhedron (right) called 'Truncated Rhombic Dodecahedron (HCR's Polyhedron)' by truncating a rhombic dodecahedron (left)

Application of HCR's Theory of Polygon — A model of Regular Penta-decahedral Solar Dome of 5mm thick acrylic sheet having 15 regular triangular faces each with side 15 cm crafted by H C Rajpoot, 26 Oct, 2021.

H C Rajpoot @ IIT Delhi — 3-D Model on Creo 5.0

H C Rajpoot @ IIT Bombay — Laser engraving on sodalime glass

Mr H. C. Rajpoot (DOB: 20 Jan, 1991), 12th Standard (Intermediate) @ Oxford Model Inter College, Syam Nagar, Kanpur (UP), India (March, 2009)

Mr H. C. Rajpoot (Doctor of Philosophy @ IIT Bombay)

Certificate of Best paper Award in Young Scholars' National Research Writing Competition 2021.

Certificate of Excellence in Peer-Reviewing for contributing to the book chapter 'Time in Mathematical Models'

Certificate of Editorial Board Membership

Certificate of Authorship for publishing Advanced Geometry in Mathematics.

Certificate of Authorship for publishing Electro-Magnetism in Physics.

This site has been created, in good faith, merely for keeping the records of biography, mathematical formulae & outstanding achievements of H.C. Rajpoot in the field of Mathematics specifically Algebra, Geometry, Trigonometry & Radiometry in Mathematical Physics.

Copyright © 2014-2025 H. C. Rajpoot. All rights reserved.